
Characteristics of Graphs of Exponential Functionsīefore we begin graphing, it is helpful to review the behavior of exponential growth.
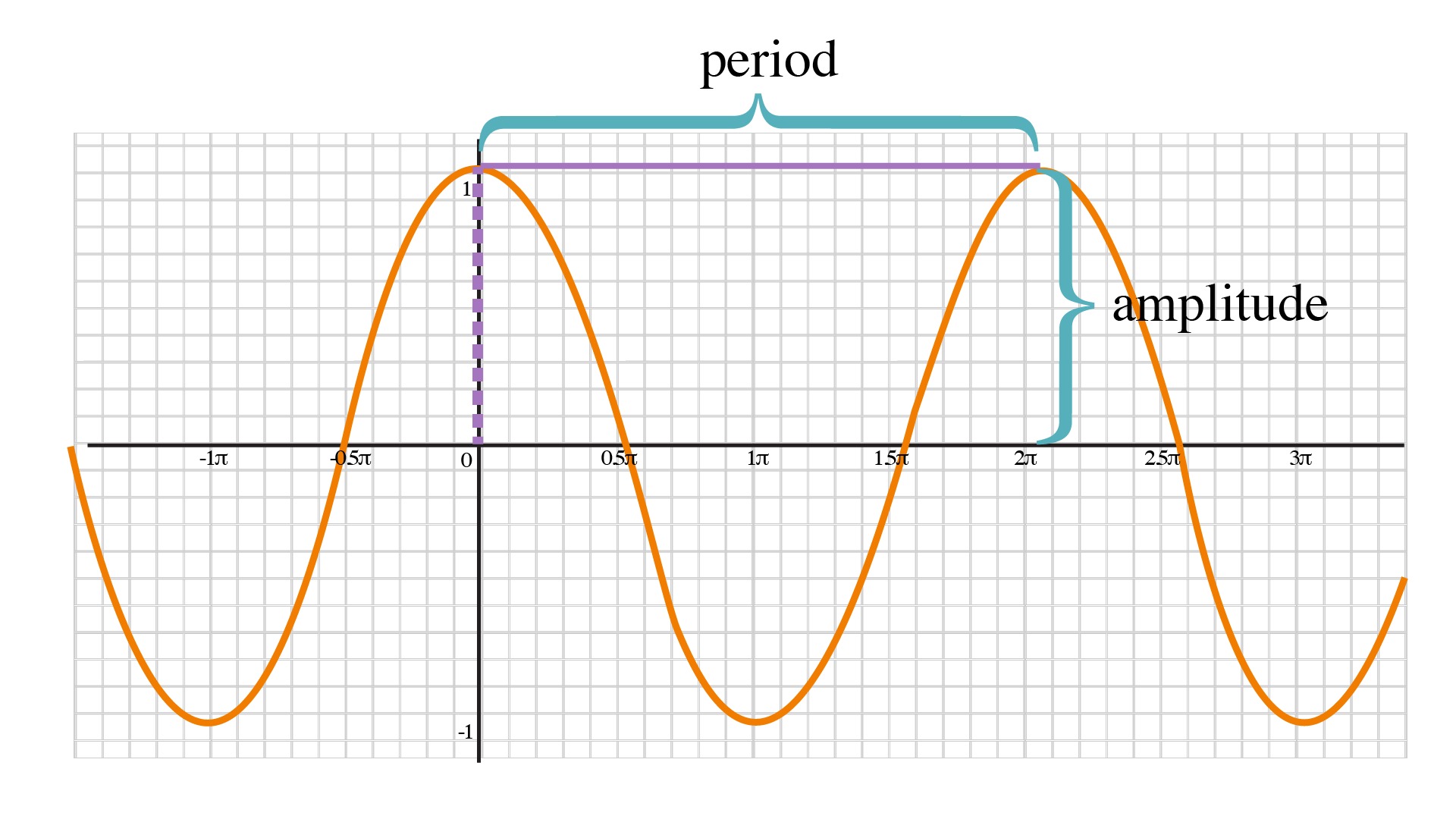
We typically construct graphs with the input values along the horizontal axis and the output values along the vertical axis. The visual information they provide often makes relationships easier to understand. Graphs display many input-output pairs in a small space. It gives us another layer of insight for predicting future events. As we have seen in examples above, we can represent a function using a graph. We learn a lot about things by seeing their visual representations, and that is exactly why graphing exponential equations is a powerful tool.

Section 2.6: Increasing and decreasing functions. Most of the time, however, the equation itself is not enough. Notice this graph has a local maximum point, but it does not have a local minimum. Working with an equation that describes a real-world situation gives us a method for making predictions. Write the equation of an exponential function that has been transformed.Īs we discussed in the previous section, exponential functions are used for many real-world applications such as finance, forensics, computer science, and most of the life sciences.Graph a reflected exponential function.For example f ( x ) 2 x + 1 and its inverse. Graph a stretched or compressed exponential function. A feature of a pair of inverse function is that their ordered pairs are reversed.
Graph exponential functions shifted horizontally or vertically and write the associated equation.For more details on some equations and functions click on the following links: linear equations, quadratic.
#Function graph generator#


 0 kommentar(er)
0 kommentar(er)
